牛顿迭代法

牛顿迭代法是用来求函数零点的一种方法，求得的结果为数值解，速度较快。

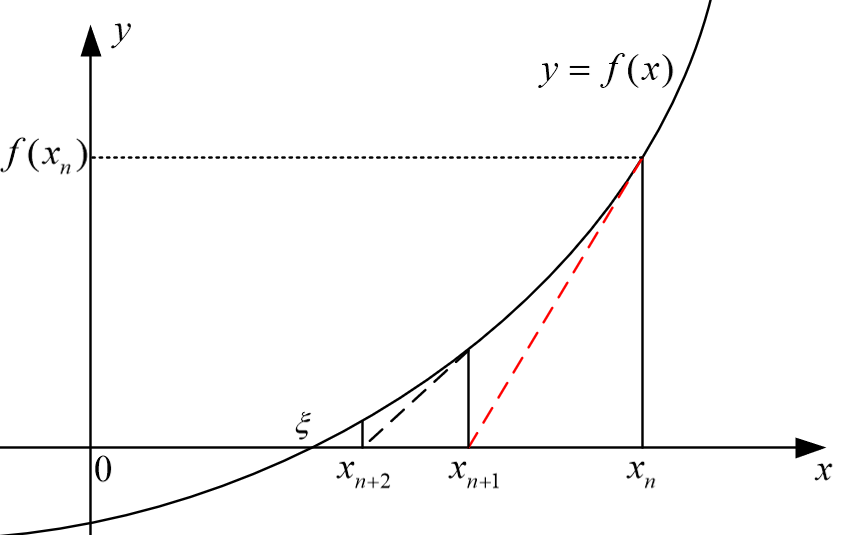
如图所示，从 x_n 开始迭代，过 (x_n, f(x_n)) 点作曲线 f(x) 的切线（图中的红色虚线），该切线的方程为

y-f(x_n)=f'(x_n)(x-x_n)

令 y=0 ，此时x的值即为 x_{n+1} 的值

0-f(x_n)=f'(x_n)(x_{n+1}-x_n)

化简可得

x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}

这就是牛顿迭代法的迭代公式，迭代次数越多则精度越高。

牛顿迭代法误差分析

那么如何知道迭代若干次后的结果的误差呢？

如图所示

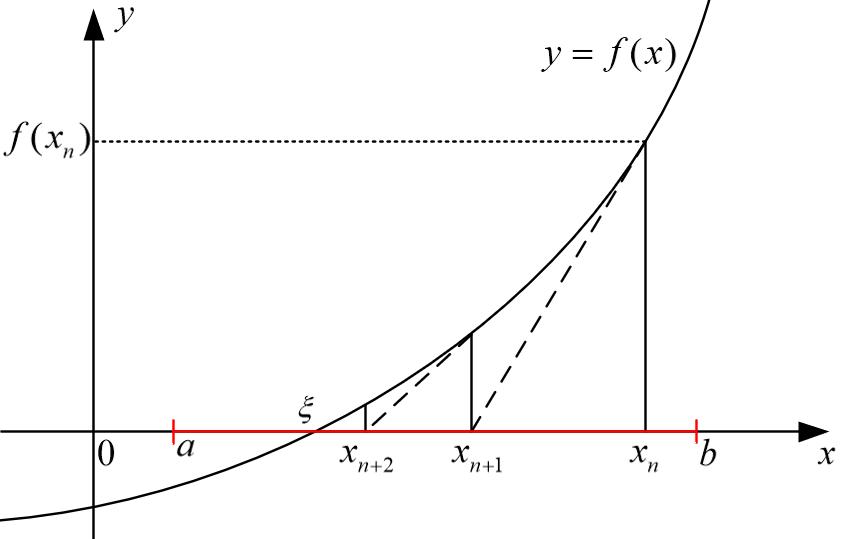
假设迭代过程中 x_n 的值始终保持在 [a, b] 的范围内，零点为 \xi ，即 f(\xi)=0 。那么根据中值定理

f(x_n)-f(\xi)=f'(\eta)(x_n-\xi), \eta介于x_n和\xi之间

可以得出

x_n-\xi=\frac{f(x_n)}{f'(\eta)}

如果取m为区间 [a, b] 内 f'(x) 的最小值，即 m=\underset{a\le x\le b}{\min} f'(x) ，那么可以得到结果误差的上界

\left | x_n-\xi \right | \le \frac{f(x_n)}{m}

这就完成了误差分析。

若要对M开平方，首先应该构造一个函数，这个函数的零点是\sqrt M，然后选取一个初始值，开始对这个函数进行迭代，在结果满足精度要求时停止迭代。

显然可以构造函数为f(x)=x^2-M，它的零点满足上述要求。它的导数为f'(x)=2x，那么迭代公式为

x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-\frac{x_n^2-M}{2x_n}=\frac{1}{2}(x_n+\frac{M}{x_n})

假设M\ge1，那么可以令迭代区间为[1, M]，显然构造函数在这个区间内单调递增，因此

m=\min_{1\le x\le M} f'(x)=f'(1)=2

所以结果的误差可以按下面的方式表示

\left|x_n-\sqrt{M} \right|\le \frac{f(x_n)}{2}=\frac{x_n^2-M}{2}

下面来实际演练一下，以计算\sqrt 2为例。

首先选取一个初始值，该值最好选取与估计值相差不大的数，比如选取x_0=2。

下面是迭代过程

x_0=2, 误差\le 1

x_1=\frac{2+\frac{2}{2}}{2}=\frac{3}{2}=1.5, 误差\le \frac{1}{8}=0.125

x_2=\frac{\frac{3}{2}+\frac{2}{\frac{3}{2}}}{2}=\frac{17}{12}=1.4166\cdots, 误差\le \frac{1}{288}=0.003472\cdots

x_3=\frac{\frac{17}{12}+\frac{2}{\frac{17}{12}}}{2}=\frac{577}{408}=1.41421\cdots, 误差\le \frac{1}{332928}=0.000003\cdots

x_4=\frac{\frac{577}{408}+\frac{2}{\frac{577}{408}}}{2}=\frac{665857}{470832}=1.41421356237\cdots, 误差\le \frac{1}{443365544448}=0.000000000002\cdots

仅迭代了4次，精度就已经到了10^{-11}，可见这个算法的速度还是比较快的。（计算过程为保证精度所以避免除法运算，而使用分数运算，只有在停止迭代时才进行一次除法运算。这也为手算提供了可能性。~~闲得无聊可以算算打发时间（bushi）~~。）